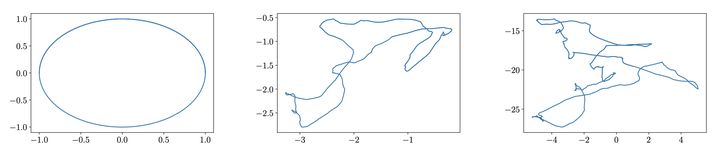
Trajectory growth lower bounds for random sparse deep ReLU networks

Abstract

This paper considers the growth in the length of one-dimensional trajectories as they are passed through deep ReLU neural networks, which, among other things, is one measure of the expressivity of deep networks. We generalise existing results, providing an alternative, simpler method for lower bounding expected trajectory growth through random networks, for a more general class of weights distributions, including sparsely connected networks. We illustrate this approach by deriving bounds for sparse-Gaussian, sparse-uniform, and sparse-discrete-valued random nets. We prove that trajectory growth can remain exponential in depth with these new distributions, including their sparse variants, with the sparsity parameter appearing in the base of the exponent.